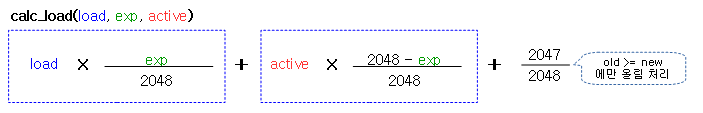Scheduler -2- (Global Cpu Load)

문영일 리눅스 커널

<kernel v5.4>

Scheduler -2- (Global Cpu Load)

cpu 로드 관련 소스의 위치는 다음과 같은 변화가 있어왔다.

 

추세 관련 사전 산술 지식

주식 시장에서 주가 흐름에 단순이동평균(SMA), 가중이동평균(WMA), 지수이동평균(EMA) 등을 사용하여 기간별 평균흐름을 나타내는데 먼저 머리를 정리하기 위해 다음과 같은 방법이 있음을 미리 산출해보자.

  • 예) 최근 6일간 종가(raw data): 1020, 1030, 1000, 1010, 1020, 1060일 때
    • 3일 단순 이동 평균(SMA: Simple Moving Average)
      • 과거 데이터와 최근 데이터를 고르게 반영
      • = (1010 + 1020 + 1060) / 3
      • = 1030
    • 3일 가중 이동 평균(WMA; Weighted Moving Average)
      • 최근 데이터에 높은 가중치를 주는 방법 (예: w1=1/6, w2=2/6, w3=3/6)
      • = 1010 * w1 + 1020 * w2 + 1060 * w3
      • = 168 + 340 + 530
      • = 1038
    • 3일 지수 이동 평균(EMA: Exponential Moving Average 또는 EWMA: Exponential Weighted Moving Average)
      • 최근 데이터에 더 높은 가중치를 주는 방법으로 전일 지수 이동 평균 값과 금일 값만 사용하여 간단히 계산한다.
      • 지수 평활 계수(Exponential Percentage) k를 사용하여 1-k를 전일 지수 이동 평균값에 곱하여 사용하고, 금일 값에 k를 곱해 사용한다.
        • 평활 계수는 다음과 같은 지수 함수 모델을 사용한다. (n=기간)
          • k = a * (b^n)
      • 지수 평활 계수(Exponential Percentage) k는 환경에 따라 다르다.
      • 주식 시장의 평활 계수 k는 지수 평균 기간에 의한 추정법을 사용하여 다음과 같이 결정된다.
        • (a=2, b=1/(n+1))
        • k= 2 * 1/(n+1) = 2/(n+1)
          • 예: n=2일, k=2/(n+1)=0.666666…
          • 예: n=3일, k=2/(n+1)=0.5
          • 예: n=10일, k=2/(n+1)=0.181818…
      • 매일 지수 이동 평균 값 * (1-k) + 금일 값 * (k)을 반영하여 산출한다.
        • 1일차: 1020 = 100% 반영
        • 2일차: 2일간 이동 평균 반영 = 1020 * 33% + 1030 * 66% = 1026
        • 3일차: 3일간 이동 평균 반영 = 1026 * 50% + 1000 * 50% = 1013
        • 4일차: 3일간 이동 평균 반영 = 1013 * 50% + 1010 * 50% = 1012
        • 5일차: 3일간 이동 평균 반영 = 1012 * 50% + 1020 * 50% = 1016
        • 6일차: 3일간 이동 평균 반영 = 1016 * 50% + 1060 * 50% = 1038
  • 가중 이동 평균과 지수 이동 평균에서 적용되는 가중치와 평활 계수가 적용 일자에 따라 변화되는 그래프 값은 다음 자료를 참고한다.

 

리눅스 커널에서의 지수 이동 평균

리눅스 커널에서는 cpu 로드 산출에 필요한 모든 raw 데이터를 저장하지 않는다. 따라서 가장 적합한 모델로 raw 데이터를 저장하지 않는 특성을 가진 지수 이동 평균(EMA)를 사용한다. 그리고 지수 평활법(ES: Exponential Smoothing) 중 하나인 지수 감소 평균(EDA)을 사용하여 지수 평활 계수 k값을 결정하는데 글로벌 cpu 로드와 PELT 산출에 사용하는 k 값이 다르며 각각의 주제에서 다루기로 한다.

  • 지수 감소 평균(EDA: Exponential Decaying Average, EDMA: Exponential Damped Moving Average)

글로벌 cpu 로드 산출식

지정된 기간에 어떠한 일을 cpu가 쉬지 않고 일을 한 경우 그 값을 1.0이라고 한다. 만일 지정된 기간에 절반 동안 idle 상태에 빠져 있으면 0.5라고 한다. 그런데 밀려 있는 일이 있으면 그 량만큼 더해 산정하여 1을 초과하게 된다.

예) 1분 동안 같은 양의 작업을 10개를 수행하는 cpu가 있다 할 때 1분 동안 30개의 작업이 주어지면 10개는 처리를 하고 20개는 처리하지 못한 상태가 된다. 이러한 경우 cpu 로드는 3.0이라 한다.

예) 위와 동일한 조건으로 cpu가 2개 준비된 경우 cpu 로드는 1.5라 한다.

 

cpu 로드의 이진화 정수 사용

cpu 로드 값은 32비트 시스템에서는 11비트를 사용한다. 실수 로드 값 1.0에 대응하는 2^11=2048 이진화 정수 값을 사용한다.

  • 1개의 cpu가 있는 시스템에서 태스크 2개가 동작 상태(runnable)인 경우 cpu 로드 값은 2.0이 된다.
  • cpu가 4개가 동작하는 시스템에서는 이 값을 cpu 수 4로 나누게 되므로 0.5의 cpu 로드 값이 된다.

 

글로벌 로드 평균 (1min ~ 15min)

최근 1분, 5분, 15분 간의 평균 cpu 로드 값을 산출하여 avenrun[]에 저장하고 글로벌 로드 평균(global load average)라고도 불린다.

  • “uptime” 명령의 load average 필드의 3개의 값을 참고한다.
  • 또한 “/proc/loadavg” 파일을 확인하여 최초 3개의 값을 통해서도 확인할 수 있다.

 

$ uptime
 20:41:18 up  1:09,  2 users,  load average: 0.57, 0.15, 0.11

$ cat /proc/loadavg 
0.55 0.28 0.16 1/318 2112
  • nr_active = 각 cpu의 런큐에 있는 running 및 uninterruptible 태스크의 수를 더한다.
  • avenrun[0] = avenrun[0]*e1 + nr_active*(1-e1) + 0.5    <- e1 = n=12(1분)에서의 지수 평활 계수 k
  • avenrun[1] = avenrun[1]*e2 + nr_active*(1-e2) + 0.5    <- e2 = n=60(5분)에서의 지수 평활 계수 k
  • avenrun[2] = avenrun[2]*e3 + nr_active*(1-e3) + 0.5    <-e3 = n=180(15분)에서의 지수 평활 계수 k

 

커널의 글로벌 cpu 로드를 위한 지수 평활 계수는 다음과 같다.

  • 지수 함수 모델 k = a * (b^n)
    • a=1, b=e^(-1/n), n=반영할 기간
  • k=e^(-1/n)
  • 지수 평활 계수 k를 사용하여 cpu 로드 값은 다음과 같이 산출된다.
    • cpu 로드 값 = 기존 cpu 로드 값 * k + 새 cpu 로드 값 * (1 – k)
  • 예) 커널이 5초에 한번씩 측정된 과거 1분 동안의 누적 데이터를 사용하므로 기간 n=12가 된다.
    • k=e^(-1/12) = 0.920044 (약 92%)
      • Excel Spread Sheet 산출 예)
        • =@exp(-1/12)

 

런큐 로드 평균 (1 tick ~ 16 ticks)

cpu 로드 밸런스에 사용하였던 이 방법은  커널 v5.3-rc1에서 제거되었다.

 

글로벌 로드 평균

avenrun[] 산출 – (1, 5, 15분)

글로벌 로드 평균은 매 스케줄 틱에서 호출되지만 산출 주기(calc_load_update: 기본 5초)에 한 번씩 갱신한다. 엄밀히 말하자면 산출 주기가 도래하면 그 후 10틱의 시간이 지난 후에 갱신한다. 글로벌 로드 평균을 산출하는 이 함수의 호출 경로는 다음과 같다. (ARM64 기준)

  • 고정 틱 핸들러
    • tick_handle_periodic() -> tick_periodic() -> do_timer() -> calc_global_load()
  • 틱 nohz 핸들러
    • tick_nohz_handler() -> tick_sched_do_timer() -> tick_do_update_jiffies64() -> do_timer() -> calc_global_load()
    • tick_nohz_update_jiffies() -> tick_do_update_jiffies64() -> do_timer() -> calc_global_load()
    • tick_nohz_restart_sched_tick() -> tick_do_update_jiffies64() -> do_timer() -> calc_global_load()
  • hrtimer 틱 핸들러
    • tick_sched_timer() -> tick_sched_do_timer() -> tick_do_update_jiffies64() -> do_timer() -> calc_global_load()

 

calc_global_load()

kernel/sched/loadavg.c

/*
 * calc_load - update the avenrun load estimates 10 ticks after the
 * CPUs have updated calc_load_tasks.
 *
 * Called from the global timer code.
 */

void calc_global_load(unsigned long ticks)
{
        unsigned long sample_window;
        long active, delta;

        sample_window = READ_ONCE(calc_load_update);
        if (time_before(jiffies, sample_window + 10))
                return;

        /*
         * Fold the 'old' NO_HZ-delta to include all NO_HZ CPUs.
         */
        delta = calc_load_nohz_fold();
        if (delta)
                atomic_long_add(delta, &calc_load_tasks);

        active = atomic_long_read(&calc_load_tasks);
        active = active > 0 ? active * FIXED_1 : 0;

        avenrun[0] = calc_load(avenrun[0], EXP_1, active);
        avenrun[1] = calc_load(avenrun[1], EXP_5, active);
        avenrun[2] = calc_load(avenrun[2], EXP_15, active);

        WRITE_ONCE(calc_load_update, sample_window + LOAD_FREQ);

        /*
         * In case we went to NO_HZ for multiple LOAD_FREQ intervals
         * catch up in bulk.
         */
        calc_global_nohz();
}

최근 1분, 5분, 15분 주기 지수 이동 평균을 사용한 글로벌 cpu 로드를 산출하여 avenrun[]에 대입한다. 이 함수가 매 틱마다 호출되지만 실제 산출은 5초 주기로 수행한다. 엄밀히 5초 주기 이후 lockless flip 인덱스 기법을 사용하기 위해 10틱이 지난 후에 수행한다.

  • 코드 라인 6~8에서 현재 시각(jiffies)이 cpu 로드 산출 주기(5초)+10틱 이전이면 함수를 빠져나간다.
  • 코드 라인 13~15에서 현재 cpu에 대해 active 태스크 수의 변화분 delta를 얻어와서 calc_load_tasks에 반영한다.
  • 코드 라인 17~18에서 active 태스크가 있는 경우 이를 11비트 정밀도를 갖는 이진화 정수로 변환시킨다.이 값을 전일 지수 이동 평균값에 적용할 예정이다.
    • 예) cpu 로드 값이 2이라면 2048(실수 1.0)을 곱한 값을 현재 로드 값으로 반영할 예정이다.
  • 코드 라인 20~22에서 기존 cpu 로드 값인 avenrun[]과 새로 추가 반영할 cpu 로드 값인 active 값으로 각각 1분, 5분, 15분에 해당하는 지수 평활 계수 EXP_n을 사용하여 avenrun[]에 반영한다.
  • 코드 라인 24에서 다음 cpu 로드 산출 주기를 위해 5초를 더한다.
  • 코드 라인 30에서 nohz idle로 인해 다음 cpu 로드 산출 주기를 이미 초과한 경우 miss된 cpu 로드 갱신 주기 수만큼 적용하여 cpu 로드를 산출하여 avenrun[]을 다시 갱신한다.
    • 예) 20여초 nohz idle로 인해 cpu 로드를 갱신하지 못한 경우 처음 5초에 해당하는 시간의 cpu 로드가 이미 갱신되었으므로 나머지 3번에 해당하는 cpu 로드를 산출하도록 한다.

 

cpu 로드 계산을 위한 11비트 지수 상수 값

11비트 정밀도를 가진 이진화 정수값을 산출하기 위한 각종 상수들이다.

include/linux/sched/loadavg.h

/*
 * These are the constant used to fake the fixed-point load-average
 * counting. Some notes:
 *  - 11 bit fractions expand to 22 bits by the multiplies: this gives
 *    a load-average precision of 10 bits integer + 11 bits fractional
 *  - if you want to count load-averages more often, you need more
 *    precision, or rounding will get you. With 2-second counting freq,
 *    the EXP_n values would be 1981, 2034 and 2043 if still using only
 *    11 bit fractions.
 */
extern unsigned long avenrun[];         /* Load averages */
extern void get_avenrun(unsigned long *loads, unsigned long offset, int shift);

#define FSHIFT          11              /* nr of bits of precision */
#define FIXED_1         (1<<FSHIFT)     /* 1.0 as fixed-point */
#define LOAD_FREQ       (5*HZ+1)        /* 5 sec intervals */
#define EXP_1           1884            /* 1/exp(5sec/1min) as fixed-point */
#define EXP_5           2014            /* 1/exp(5sec/5min) */ 
#define EXP_15          2037            /* 1/exp(5sec/15min) */
  • FSHIFT
    • 11비트 정확도를 사용하는데 필요한 비트 수
  • FIXED_1
    • 11비트 정확도 값 (2048)
    • 고정 소숫점 형태인 cpu 로드 1.0은 리눅스 구현에서는 2048이라는 이진화 정수로 표현한다.
  • LOAD_FREQ
    • 디폴트 5초 주기 산출
  • EXP_1
    • 마지막 1분 동안의 cpu 로드를 산출하기 위해 11비트 정확도 값 2048의 약 92%를 적용하여 반영한다.
    • 1/(exp(1/12)) * FIXED_1 = 92.00% * 2048 = 1884
  • EXP_5
    • 마지막 5분 동안의 cpu 로드를 산출하기 위해 11비트 정확도 값 2048의 약 98%를 적용하여 반영한다.
    • 1/(exp(1/60)) * FIXED_1 = 98.35% * 2048 = 2014
  • EXP_15
    • 마지막 15분 동안의 cpu 로드를 산출하기 위해 11비트 정확도 값 2048의 약 99%를 적용하여 반영한다.
    • 1/(exp(1/180)) * FIXED_1 = 99.45% * 2048 = 2037

 

다음 그림은 1분, 5분, 15분에 해당하는 지수 팩터 EXP_1, EXP_5, EXP_15가 어떻게 산출되었는지를 보여준다.

  • k(12) = EXP_1 = 0.9200 (=1884)
  • k(60) = EXP_5 = 0.9835 (=2014)
  • k(180) = EXP_15 = 0.9945 (=2037)

 

다음 그림은 글로벌 cpu 로드를 산출하는 식을 보여준다. (커널 v4.7~)

 

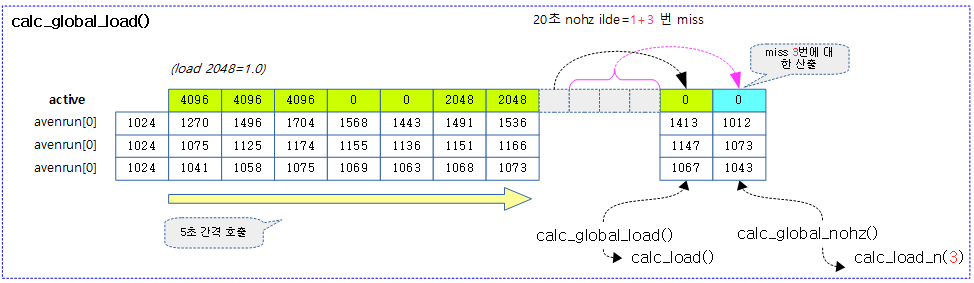
다음 그림은 처음 cpu 로드 0.5에서 출발하여 매 5초 마다 cpu 로드가 산출되는 과정을 보여주며 마지막에서는 nohz idle로 인해 20초간 틱이 발생되지 않아 밀려 있는 cpu 로드 계산이 한꺼번에 이루어지는 것을 보여준다.

  • 주의: 커널 v4.6 이하에서 반올림이 적용되어 산출한 값이다. 커널 v4.7 이상에서는 새 로드가 기존 로드보다 동등하거나 상승하는 경우 올림처리한다.

 

active 태스크 수 이론

cpu 로드를 산출하기 위해 active 태스크 수를 파악해야 한다. 리눅스에서의 active 태스크 수는 다음을 포함한다.

  • runnable 태스크 수
    • running 태스크(rq->curr 태스크)
    • 런큐에서 엔큐되어 대기중인 태스크들
  • uninterruptible 상태로 슬립한 태스크 수

 

리눅스 시스템에서의 글로벌 cpu 로드는 cpu 로드라기 보다는 시스템 로드에 더 가깝다. cpu 로드를 산출하기 위해 active 태스크 수를 파악해야 한다.

  • active 태스크 산출 요소
    • runnable 태스크의 수
      • running 태스크 (cfs_rq->curr 엔티티)
      • RB Tree enqueue 태스크들
      • 유닉스 및 리눅스에서 사용
    • Sleep 상태의 uninterruptible 태스크(주로 io 요청 대기 스레드) 수
      • 리눅스에서만 사용

 

유닉스 등과 다르게 리눅스에서는 uninterruptible 상태로 슬립 중인 태스크도 포함시키는 이유로 로드를 산출하는데 이 uninterruptible 태스크가 I/O 요청에 대한 대기 상태인 경우가 많고 이에 따라 I/O 요청에 대한 로드를 포함하는 것이 합리적인 판단이라서 포함시켰다.  확실히 이와 같은 형태의 글로벌 로드 산출 구현은 정확한 로드를 산출하는 것이 힘들다는 것을 알 수 있다. 그러므로 cpu 글로벌 로드 뿐만 아니라 여러 상태 지표를 동시에 사용하여야 시스템의 로드 상태를 파악할 수 있다. (결국 지금도 완전하지 않은 상태로 추후 바뀔 가능성도 있다)

 

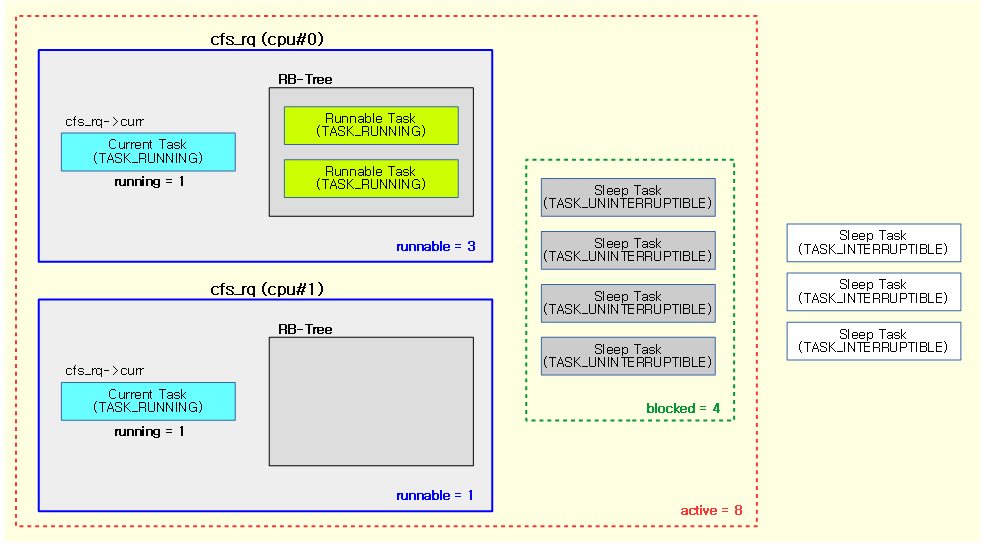
다음 그림은 루트 태스크 그룹만을 가진 2개 cpu에서 동작하는 각 cfs 런큐의 태스크 상태들을 보여준다. 이들 중 로드에 포함될 active 태스크 수는 8이다.

  • 로드에 포함될 태스크들 (총 8개)
    • 4 개의 runnable 태스크들
      • 2 개의 running 태스크들
      • 2 개의 enqueue 태스크들
    • 4 개의 슬립 태스크들
      • 4 개의uninterruptible 태스크들

 

런큐에서의 active 태스크 수 산출 실전

active 태스크 수를 산출할 때 마다 각 cpu의 런큐를 뒤지지 않고 전역 변수 calc_load_tasks에 필요 시마다 전파하여 사용하는 방식을 사용하여 조금이라도 빠른 산출 방법을 적용하였다. nohz idle을 위해 중간 단계에 calc_load_nohz[2] 변수를 사용하여 active 태스크의 변동 분 delta를 저장하고 5초마다 로드가 산출될 때 calc_load_nohz[2] 배열에서 인덱스를 교대로 사용하여 읽어낸다. 배열의 사용법은 조금 복잡하니 calc_load_nohz_fold()에서 더 알아보자.

 

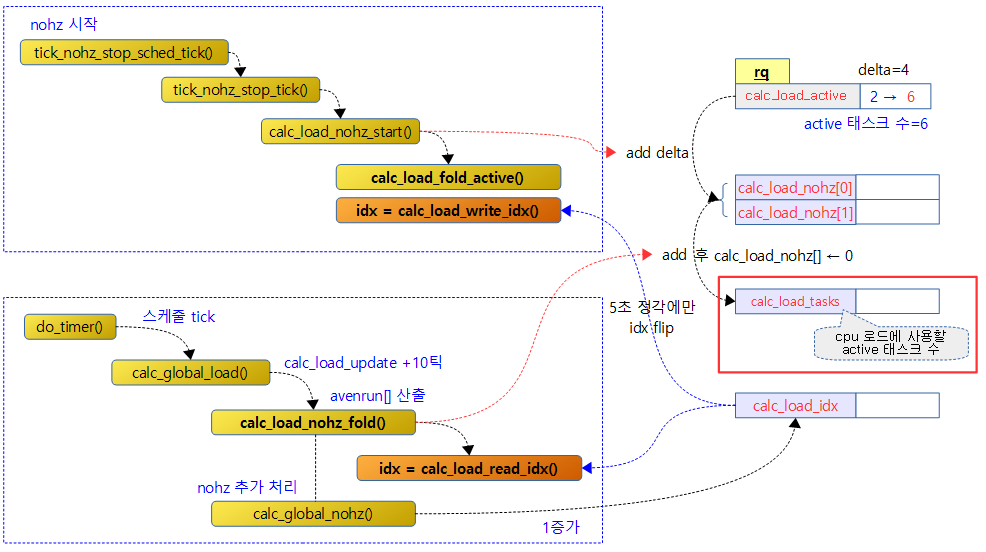
다음 그림은 nohz idle 상태로 진입할 때 active 태스크의 변동분을 저장하는 함수와 5초 주기로 글로벌 로드를 산출하는 함수의 흐름을 보여준다.

 

calc_load_nohz_fold()

kernel/sched/loadavg.c

static long calc_load_nohz_fold(void)
{
        int idx = calc_load_read_idx();
        long delta = 0;
        
        if (atomic_long_read(&calc_load_nohz[idx]))
                delta = atomic_long_xchg(&calc_load_nohz[idx], 0);

        return delta;
}

현재 cpu의 런큐에서 다시 계산된 active 태스크 수의 변경된 값 delta를 얻어온다. (lockless를 위해 flip 인덱스로 접근하도록 설계되었다.)

  • 코드 라인 3에서 calc_load_nohz[] 배열 중 어떤 값을 사용할지 인덱스 값을 알아온다.
  • 코드 라인 6에서 인덱스에 해당하는 calc_load_nohz[] 값이 존재하는 경우 이 값을 0으로 초기화하고 저장되었던 값을 반환한다.

 

calc_load_nohz[]

kernel/sched/loadavg.c

/*
 * Handle NO_HZ for the global load-average.
 *
 * Since the above described distributed algorithm to compute the global
 * load-average relies on per-CPU sampling from the tick, it is affected by
 * NO_HZ.
 *
 * The basic idea is to fold the nr_active delta into a global NO_HZ-delta upon
 * entering NO_HZ state such that we can include this as an 'extra' CPU delta
 * when we read the global state.
 *
 * Obviously reality has to ruin such a delightfully simple scheme:
 *
 *  - When we go NO_HZ idle during the window, we can negate our sample
 *    contribution, causing under-accounting.
 *
 *    We avoid this by keeping two NO_HZ-delta counters and flipping them
 *    when the window starts, thus separating old and new NO_HZ load.
 *
 *    The only trick is the slight shift in index flip for read vs write.
 *
 *        0s            5s            10s           15s
 *          +10           +10           +10           +10
 *        |-|-----------|-|-----------|-|-----------|-|
 *    r:0 0 1           1 0           0 1           1 0
 *    w:0 1 1           0 0           1 1           0 0
 *
 *    This ensures we'll fold the old NO_HZ contribution in this window while
 *    accumlating the new one.
 *
 *  - When we wake up from NO_HZ during the window, we push up our
 *    contribution, since we effectively move our sample point to a known
 *    busy state.
 *
 *    This is solved by pushing the window forward, and thus skipping the
 *    sample, for this CPU (effectively using the NO_HZ-delta for this CPU which
 *    was in effect at the time the window opened). This also solves the issue
 *    of having to deal with a CPU having been in NO_HZ for multiple LOAD_FREQ
 *    intervals.
 *
 * When making the ILB scale, we should try to pull this in as well.
 */

static atomic_long_t calc_load_nohz[2];
static int calc_load_idx;

 

nohz idle 영향으로 인해 변경된 해당 cpu의 active 태스크 수 delta 값을 calc_load_nohz[2]에 저장을 하는데 저장 위치는 5초 갱신 주기마다 교대로 바뀐다. 이러한 delta 값을 읽어내는 루틴에서는 매 5초 + 10 틱마다 지난 5초 이내에 변동된 delta 값을 읽어낸다. 읽어내는 시점의 10 tick 범위는 다음에 읽도록 한다.

  • calc_load_read_idx() 함수를 통해 calc_load_idx 값의 하위 1비트만 읽어서 0과 1의 인덱스 값으로 calc_load_nohz[] 값을읽어온다.
  • 매 5초+10틱에서 calc_load_idx 값을 증가시킨다.
  • calc_load_write_idx() 함수를 통해 calc_load_idx 값의 하위 1비트만 읽어내는데 10 tick 구간은 flip 시킨다. 이렇게 알아온 0과 1의 인덱스 값으로 calc_load_nohz[] 값을읽어온다.

 

calc_load()

kernel/sched/loadavg.c

/*
 * a1 = a0 * e + a * (1 - e)
 */
static inline unsigned long
calc_load(unsigned long load, unsigned long exp, unsigned long active)
{
        unsigned long newload;

        newload = load * exp + active * (FIXED_1 - exp);
        if (active >= load)
                newload += FIXED_1-1;

        return newload / FIXED_1;
}

지수 이동 평균 기간이 적용된 지수 평활 계수 @exp를 사용하여 새 로드 값을 산출한다.

  • 코드 라인 5에서 기존 로드 값 @load에 이동 평균 기간이 적용된 지수 평활 계수 @exp를 곱해 감소시킨 후 현재 로드 값인 active 값을 반영한다.
    • @load 값은 기존 로드 값으로 11비트 정확도를 사용한 이진화 정수 값이다.
    • @active 값은 반영할 현재 로드 값으로 11비트 정확도를 사용한 이진화 정수 값이다.
  • 코드 라인 6~9에서 반영할 로드 값이 기존 로드 값보다 더 큰 경우 상승 추세이므로 소숫점이하 올림 처리하고, 그 외에는 버린다.

 

다음 그림은 글로벌 cpu 로드를 산출하는 예를 보여준다. (커널 v4.7~)

 

예) 기존 1,5,15분간 cpu 로드=0.5이고 이번 틱에 active 태스크=2인 상태로 3번의 틱 만큼 진행을 하면

  • 산출 전:
    • avenrun[0]=1024, active=4096
    • avenrun[1]=1024, active=4096
    • avenrun[2]=1024,active=4096
  • 1st 틱:
    • avenrun[0]=(1024 * 1884 + 4096 * (2048-1884) + 2047) / 2048 = 1270
    • avenrun[1]=(1024 * 2014 + 4096 * (2048-2014) + 2047) / 2048 = 1075
    • avenrun[2]=(1024 * 2037 + 4096 * (2048-2037) + 2047) / 2048 = 1041
  • 2nd 틱:
    • avenrun[0]=(1271 * 1884 + 4096 * (2048-1884) + 2047) / 2048 = 1497
    • avenrun[1]=(1076 * 2014 + 4096 * (2048-2014) + 2047) / 2048 = 1126
    • avenrun[2]=(1041 * 2037 + 4096 * (2048-2037) + 2047) / 2048 = 1058
  • 3rd 틱:
    • avenrun[0]=(1498 * 1884 + 4096 * (2048-1884) + 2047) / 2048 = 1706
    • avenrun[1]=(1127 * 2014 + 4096 * (2048-2014) + 2047) / 2048 = 1176
    • avenrun[2]=(1058 * 2037 + 4096 * (2048-2037) + 2047) / 2048 = 1075

 

예) 기존 1,5,15분간 cpu 로드=0.5이고 이번 틱에 active 태스크=0인 상태로 3번의 틱 만큼 진행을 하면

  • 산출 전:
    • avenrun[0]=1024, active=0
    • avenrun[1]=1024, active=0
    • avenrun[2]=1024,active=0
  • 1st 틱:
    • avenrun[0]=(1024 * 1884 + 0 * (2048-1884) + 0) / 2048 = 942
    • avenrun[1]=(1024 * 2014 + 0 * (2048-2014) + 0) / 2048 = 1007
    • avenrun[2]=(1024 * 2037 + 0 * (2048-2037) + 0) / 2048 = 1018
  • 2nd 틱:
    • avenrun[0]=(1271 * 1884 + 0 * (2048-1884) + 0) / 2048 = 866
    • avenrun[1]=(1076 * 2014 + 0 * (2048-2014) + 0) / 2048 = 990
    • avenrun[2]=(1041 * 2037 + 0 * (2048-2037) + 0) / 2048 = 1012
  • 3rd 틱:
    • avenrun[0]=(1498 * 1884 + 0 * (2048-1884) + 0) / 2048 = 796
    • avenrun[1]=(1127 * 2014 + 0 * (2048-2014) + 0) / 2048 = 973
    • avenrun[2]=(1058 * 2037 + 0 * (2048-2037) + 0) / 2048 = 1006

 

cpu 로드 소숫점 처리

글로벌 cpu 로드를 처리하는데 장시간 idle 상태인데에도 각 주기별로 0.00, 0.01, 0.05 이하 값이 더 이상 하강하지 않는 버그가 있어 수정하였다.

  • 커널 v4.7이후 현재 코드와 동일하게 상승시 올림 처리하고, 하강시 내림 처리한다.
  • 커널 v4.7 이전 코드들은 상승/하강시 모두 반올림 처리하였다.
    • load *= exp;
    • load += active * (FIXED_1 – exp);
    • load += 1UL << (FSHIFT – 1);
    • return load >> FSHIFT;

 

다음 그림은 로드 값의 변화를 산출할때 반올림하여 처리하는 모습을 보여준다. (커널 v4.6 이하)

 

calc_global_nohz()

kernel/sched/loadavg.c

/*
 * NO_HZ can leave us missing all per-CPU ticks calling
 * calc_load_fold_active(), but since a NO_HZ CPU folds its delta into
 * calc_load_nohz per calc_load_nohz_start(), all we need to do is fold
 * in the pending NO_HZ delta if our NO_HZ period crossed a load cycle boundary.
 *
 * Once we've updated the global active value, we need to apply the exponential
 * weights adjusted to the number of cycles missed.
 */

static void calc_global_nohz(void)
{
        unsigned long sample_window;
        long delta, active, n;

        sample_window = READ_ONCE(calc_load_update);
        if (!time_before(jiffies, sample_window + 10)) {
                /*
                 * Catch-up, fold however many we are behind still
                 */
                delta = jiffies - sample_window - 10;
                n = 1 + (delta / LOAD_FREQ);

                active = atomic_long_read(&calc_load_tasks);
                active = active > 0 ? active * FIXED_1 : 0;

                avenrun[0] = calc_load_n(avenrun[0], EXP_1, active, n);
                avenrun[1] = calc_load_n(avenrun[1], EXP_5, active, n);
                avenrun[2] = calc_load_n(avenrun[2], EXP_15, active, n);

                WRITE_ONCE(calc_load_update, sample_window + n * LOAD_FREQ);
        }

        /*
         * Flip the NO_HZ index...
         *
         * Make sure we first write the new time then flip the index, so that
         * calc_load_write_idx() will see the new time when it reads the new
         * index, this avoids a double flip messing things up.
         */
        smp_wmb();
        calc_load_idx++;
}

nohz idle로 인해 갱신이 밀려 있는 경우 그 밀려 있는 횟수 만큼 한 번에 산출을 하여 avenrun[]에 대입한다.

  • 코드 라인 6~7에서 현재 시간(jiffies)이 갱신 주기+10틱보다 뒤에 있는 경우 즉, 갱신이 밀려 있는 경우
  • 코드 라인 11~12에서 몇 번 밀려 있는지 횟수를 산출한다.
    • 예) jiffies와ㅓ calc_load_update의 차이가 21초인 경우 21/5+1 = 정수 5가된다.
  • 코드 라인 14~15에서 현재 active 태스크 수를 읽어와서 그 값을 11비트 정밀도를 가진 이진화 정수로 바꾼다.
  • 코드 라인 17~21에서 avenrun[] 값을 갱신하고 갱신 주기도 update한다.
  • 코드 라인 32에서 calc_load_idx를 증가시켜 새로운 인덱스를 사용하도록 한다.

 

calc_load_n()

kernel/sched/loadavg.c

/*
 * a1 = a0 * e + a * (1 - e)
 *
 * a2 = a1 * e + a * (1 - e)
 *    = (a0 * e + a * (1 - e)) * e + a * (1 - e)
 *    = a0 * e^2 + a * (1 - e) * (1 + e)
 *
 * a3 = a2 * e + a * (1 - e)
 *    = (a0 * e^2 + a * (1 - e) * (1 + e)) * e + a * (1 - e)
 *    = a0 * e^3 + a * (1 - e) * (1 + e + e^2)
 *
 *  ...
 *
 * an = a0 * e^n + a * (1 - e) * (1 + e + ... + e^n-1) [1]
 *    = a0 * e^n + a * (1 - e) * (1 - e^n)/(1 - e)
 *    = a0 * e^n + a * (1 - e^n)
 *
 * [1] application of the geometric series:
 *
 *              n         1 - x^(n+1)
 *     S_n := \Sum x^i = -------------
 *             i=0          1 - x
 */
static unsigned long
calc_load_n(unsigned long load, unsigned long exp,
            unsigned long active, unsigned int n)
{

        return calc_load(load, fixed_power_int(exp, FSHIFT, n), active);
}

기존 load 값에 새 active 값이 exp(간격)으로 FSHIFT(2048) 정확도로 산출한다.

  • 예) exp=1884(1분 주기), FSHIFT=2048(정확도), load=1024, active=2048, n=4
    • = load * (exp / FSHIFT) + (active * (FSHIFT – exp) / 2048) + 0.5 를 4번 수행
    • = load * (exp^n / 2048^n) + (active * (1 – (exp^n / 2048^n)) + 0.5와 동일
    • = 1024 * (1884^4 / 2048^4) + (active * (1 – (1884^4) / 2048^4) + 0.5
    • = 1896

 

active 태스크 수가 변함 없이 n 번의 횟수만큼 계산되는 결과와 동일하다.

 

fixed_power_int()

kernel/sched/loadavg.c

/**
 * fixed_power_int - compute: x^n, in O(log n) time
 *
 * @x:         base of the power
 * @frac_bits: fractional bits of @x
 * @n:         power to raise @x to.
 *
 * By exploiting the relation between the definition of the natural power
 * function: x^n := x*x*...*x (x multiplied by itself for n times), and
 * the binary encoding of numbers used by computers: n := \Sum n_i * 2^i,
 * (where: n_i \elem {0, 1}, the binary vector representing n),
 * we find: x^n := x^(\Sum n_i * 2^i) := \Prod x^(n_i * 2^i), which is
 * of course trivially computable in O(log_2 n), the length of our binary
 * vector.
 */
static unsigned long
fixed_power_int(unsigned long x, unsigned int frac_bits, unsigned int n)
{
        unsigned long result = 1UL << frac_bits;

        if (n) for (;;) {
                if (n & 1) {
                        result *= x;
                        result += 1UL << (frac_bits - 1);
                        result >>= frac_bits;
                }
                n >>= 1;
                if (!n)
                        break;
                x *= x;
                x += 1UL << (frac_bits - 1);
                x >>= frac_bits;
        }

        return result;
}

(x^n) / (2^frac_bits)^(n-1) 를 산출한다. 산출 시 n번 만큼 반복하지 않고 O(log2 n)번으로 산출되는 것이 특징으로 n 값이 클 때 효과적이다.

  • 예) x=1884 (EXP_1), frac_bits=11 (11비트 정밀도), n=5
    • = (1884 * 1884 * 1884 * 1884 * 1884) / (2048 * 2048 * 2048 * 2048) = 1,349

 

참고

 

 

댓글 남기기